
BackTracking 백트래킹 = 퇴각검색
백트래킹은 한정 조건을 가진 문제를 풀려는 전략이다.
1950년대 미국 수학자 D.H.레머가 만들었다.

한정 조건을 가진 경우 원소의 순서는 해결 방법과 무관하다. 이런 문제는 변수 집합으로 이뤄지는데,
한정 조건을 구성하려면 각가의 변수들을 값이 있어야 한다. 퇴각 검색은 모든 조합을 시도해서
문제의 해를 찾는다. 이것이 장점이 될 수 있는 이유는
퇴각검색 구현 방법들이 많은 부분 조합들을 배제하기때문이다.
결국 풀이 시간이 단축된다.
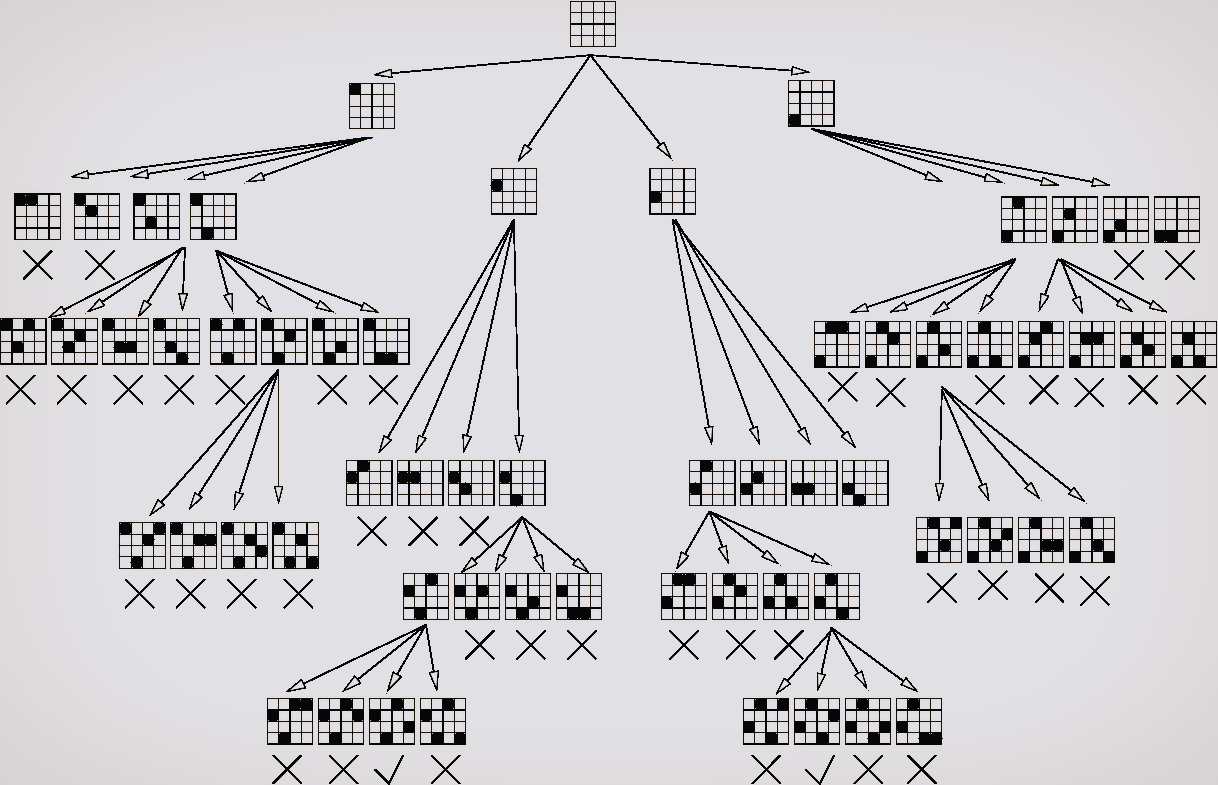
주요 개념은 해를 얻을 때까지 모든 가능성을 시도한다는 점이다.
모든 가능성은 하나의 트리처럼 구성할 수 있으며, 가지 중에 해결책이 있다.
트리를 검사하기 위해 DFS를 사용한다.
탐색 중 오답을 만나면 이전 분기점으로 돌아간다.
시도해보지 않은 다른 해결 방법이 있으면 시도한다.
해결 방법이 더 없으면 더 이전의 분기점으로 돌아간다.
모든 트리의 노드를 검사해도 답을 못찾을 경우, 이 문제의 해결잭은 없는 것이다.
백트래킹은 보통 재귀함수로 구현한다. 퇴각검색은 DFS 와 대략 같으나 기억 공간은 덜 차지 한다. ( DFS의 약간의 차이점) 백트래킹은 현재의 상태를 보관하고 바꾸는 동안만 차지하는 동작을 한다.
탐색 속도를 높이기 위해
재귀 호출을 하기 전에 시도할 값을 정하고 조건을 벗어난 값을 지우는 알고리즘을 적용할 수 있다.
아니면,
그 값을 제외한 다른 값들을 탐색할 수 있다.
백트래킹은 DFS에서 원하는 답의 가능성을 판단하고 더 깊이 탐색할지 말지 결정하면서 움직인다.
잘 만들으면, 더 효율적인 알고리즘이 나온다고 보면되겠다.
대표적인 백트래킹 문제 N-Queens 문제를 보자.
우선 훌륭한 블로그를 참고하는게 더 좋다.
n = int(input())
s = [0 for i in range(16)]
result = 0
def isTrue(x):
for i in range(1, x):
if s[x] == s[i] or abs(s[x] - s[i]) == x - i:
return False
return True
def dfs(cnt):
global result
if cnt > n:
result += 1
else:
for i in range(1, n + 1):
s[cnt] = i
if isTrue(cnt):
dfs(cnt + 1)
dfs(1)
print(result)
'Algorithm > Algorithm' 카테고리의 다른 글
| 🧩 코딩 테스트 정복기 @21#B*06 (0) | 2021.02.18 |
|---|---|
| 🧩 코딩 테스트 정복기 @21#B*05 (1) | 2021.02.01 |
| 🧩 코딩 테스트 정복기 @21#B*04 (0) | 2021.01.31 |
![[백트래킹] 퇴각검색](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F5mF2C%2FbtqXKuREpzH%2FsjQYwNCDTXF46ljAgMG7MK%2Fimg.png)